United States News
See other United States News Articles
Title: Forensic acoustic proof of SECOND shooter in the Las Vegas massacre
Source:
[None]
URL Source: https://www.youtube.com/watch?v=JxmEFeKy8aI
Published: Oct 11, 2017
Author: Mike Adams TheHealthRanger
Post Date: 2017-10-11 00:40:47 by A K A Stone
Keywords: None
Views: 51482
Comments: 148
Post Comment Private Reply Ignore Thread
Top • Page Up • Full Thread • Page Down • Bottom/Latest
Begin Trace Mode for Comment # 97.
#1. To: nolu chan, VXH, buckeroo, tooconservative, cz82, redleghunter (#0)
Found this interesting video.
Adams assumes a shooter using an AR-15 with .223 Remington 55 grain ammo. He states 20% humidity. He states a 925 m/s bullet velocity which is ~3034.8 fps. He specifies a 16.5" barrel, but a 3034.8 fps initial velocity would seem to indicate a 20" barrel or different ammo. I believe the white board has an error. The flight time should be 0.532s, not 0.528s. It lists both the 400 yard flight time and the lag time as 0.528s. This would mean the bullet velocity was precisely double the speed of sound, and that double 0.528s, or 1.056s would be the 400 yard travel time for the speed of sound. The time of sound travel for 400 yards at 1130 fps is 1.062. http://gundata.org/blog/post/223-ballistics-chart/ He cites his use of a gundata ballistics chart for travel time. gundata indicates for 400 yards, the time of travel is 5.32s, specifying a standard 55gr Remington .223 bullet leaving the barrel at 3,215fps. Adams also specified a 16.5 inch barrel, but it seems an AR-15 with a 16.5 barrel does not achieve 3,215 initial velocity. Testing with different barrel lengths indicates an AR-15, 16.5" barrel, with Remington .223 ammo, does not achieve 3,034.8 muzzle ("initial") velocity. With a 20" barrel, the same setup gets 3,071 fps muzzle velocity. A 25" barrel gets it up to 3,221 fps muzzle velocity. A 16.5" with Federal M193/55 gets 3,187 fps muzzle velocity. http://guide.sportsmansguide.com/ballistic-chart/remington_charts/223rembal.htm A ballistics chart indicates that a Remington .223 will not get the stated bullet velocity. Assuming the shots were fired from room 32135, and that end of the Mandalay Bay Hotel was 1208 feet from the base of the bandstand, and that a bullet struck the pavement at or near the base of the bandstand, the long side a right triangle would be 1208 feet and the short side would be the height of room 32135. The building claims a height of 480 feet and 44 stories, for an average of 10.91 feet per story. The 32nd floor would be 338.21 feet up. (31 x 10.91, base of floor 1 has zero height). With sides of 1208 and 338.21, the hypotenuse would be 1254.45 feet. The actual distance the bullet traveled would be more than that as it would not follow a straight path, but would follow an arc. Using estimates of distance to striking the venue surface of ~1250 feet, and detected lag times of 0.559 sec and 0.374 sec, the slower bullet made the 0.374 lag time; the faster bullet arrived .559 sec before the muzzle blast. At 1130 fps, the sound would cover 1250 feet in about 1.106 seconds. A bullet making the 1250 ft trip .559 sec before the sound, made the trip in .547 sec. A bullet making the 1250 ft trip .374 sec before the sound, made the trip in .732 sec. 1250 feet in .547 sec is an avg velocity of ~2236 fps. 1250 feet in .732 sec is an avg velocity of ~1708 fps. This assumes both shots were taken from the same location. What bullets were used can be ascertained by collecting the bullets. What was left in the room should be inventoried, along with what guns were in the room. http://onyourownadventures.com/hunttalk/showthread.php?267715-308-Ammo-Help/page2 Most mfgs recommend a minimum velocity of 1800 fps for proper expansion. The so called "magic number" associate with elk hunting is 1200 lb ft Energy. Below that is risky and I prefer 1400 lb ft as my personal standard. Although every gun is different the ammo mfg. Will put their tested numbers out for their loads. According to Federal their TBT 165 gr out of a 308 maintains 1939 fps and 1377 lb ft at 500 yards. Mathematically that should do the job as long as the bullet hits it's mark. Federal lists the same weight game King at 1708 FPS and 1069 ft lb at 500 yards. Obviously not the best option. If you keep 400 yards and in either a 150 or 165 gr factory loaded bonded round should work fine on elk. You just need to find the one that goes exactly where you want it to every time you press the trigger. This would suggest the possibility of the 1708 fps round being a .308 (or whatever else gets around 1708 fps at 400 - 450 yards. http://gundata.org/blog/post/223-ballistics-chart/ [...] .223 Remington, Remington Metal Case, 55gr. 400 yards This ballistics chart indicates .532 seconds for 400 yards, at 1588 velocity. .532 seconds would indicate 2255.6 average velocity for the 400 yards, and the velocity of the bullet leaving the barrel is specified at 3215 fps.
All numbers he pulled out of his arse? Plus there's the little problem that he doesn't present any actual audio evidence.
Plus there's the little problem that he doesn't present any actual audio evidence. The audio he used is presented. Your chartoon is an absurdity.
LOL. He scribbled on a whiteboard. The amplitude graphs of the audio referenced on my meme can be reproduced by anyone with minimal tools. It's REPRODUCIBLE - that's what differentiates valid science from conspiratorial buffoonery. Show us the actual amplitude graphs or STFU.
That you reproduce meaningless bullshit is meaningful, but not as you intend.
The amplitude graphs are reproducible by anyone who has simple tools and access to the video on Youtube. Where's yours?
Proving imbeciles can reproduce. As the U.S. Supreme Court observed, "Three generations of imbeciles are enough." Your chartoons, with your hilarious analysis, are entertaining, sort of like the scientific sounding youtubers preaching flat Earth theory.
The amplitude graphs are reproducible by anyone who has simple tools and access to the video on Youtube. Where's yours? { shrug } Maybe you just don't have what it takes.
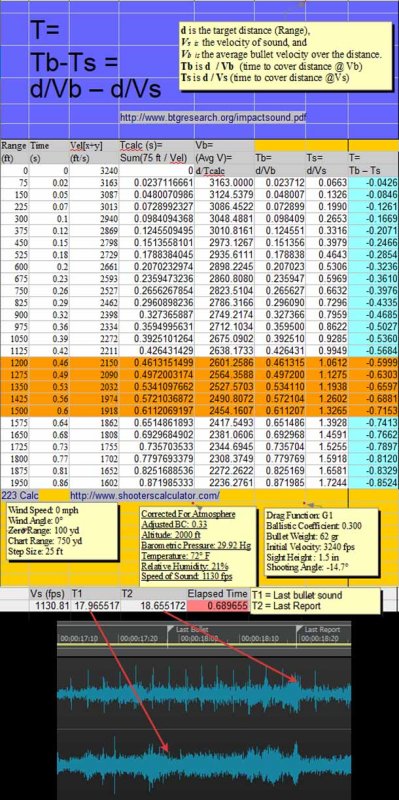
On your spreadsheet chartoon, notice that you calculate T = Tb - Ts. You calculate elapsed time as the time it took the bullet to travel, minus the time it took the sound to travel. As the bullet is supersonic, and sound is a constant, the sound would travel 400 yards in 1.06s and the bullet would travel the 400 yards in less than 1.06s. Subtracting 1.06 from a smaller number will always yield a negative number. At 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. The average donkey could recognize that something is wrong when the result is negative time. Just what do you think happens in negative 0.6126 seconds? You could at least recognize that if you get a negative number, you have stated the required formula backwards, and you proceeded to perform the calculation backwards, and present the bass ackwards result of your understanding of the study you looked at. You've got what it takes to make bullets travel in negative time. Your brain apparently has zero amplitude.
>>at 1200 feet, you actually calculate Tb as 0.448578s, and Ts as 1.062s and calculate the T as -0.6126, negative 0.6126 seconds. 0.448578 is the ballistic projectile time. 1.062 is the time to travel the same distance at the speed of sound The MEASURED, absolute value, of the Ellapsed Time difference, per the audio amplitude graph... ...between the Last Bullet sound event and the Last Report sound event is 0.689655 Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
No Absolute value is ever expressed as a negative number. Had your undisclosed formula for the last column of your spreadsheet included code to express an absolute value, your spreadsheet results would not appear as negative numbers. But your spreadsheet displays negative numbers and you did not even question it or fix your spreadsheet. The results should all be positive, like this: d = distance 400 yards, 1200 feet Column 1 = d/FPS = time in seconds Row 1 = directly inserted data. Data display is set to show 3 decimal places. Row 2 = spreadsheet formulas The formulas for Row 2 are dragged down to generate Rows 3-30.
>>No Absolute value is ever expressed as a negative number. =========== Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute. Range corresponds to the ABSOLUTE value of the difference in time.
I know. They have a spreadsheet function for that. It has been around since Lotus 123 and Quatro. ABS(number).
Yes, but in this case the ABS is implied in knowledge of what the spreadsheet is actually calculating. If you applied ABS(Tb-Ts-) the chart would loose the information regarding whether the Vb was super-sonic or not, which the negative numbers conveniently tell us. The author's formula works just fine without your tweakage. http://ww w.btgresearch.org/AcousticReconstruction02042012.pdf And that IS the same formula I have in my illustration:
Why do you keep posting this chartoon when all your data is not only wrong, but farcical? The only things you proved is that you do not know how to calculate the average velocity of an imaginary bullet and you are hopeless at spreadsheets. Your entertainment value as a useful idiot is over for now, and you will never figure it out without more help. Help is on the way, grasshopper. Columns 1, 2, and 3 are direct entry of data generated by entering imaginary data into a generator at http://www.shooterscalculator.com/. I replicated the data taken from the calculator with “My BB's.” If I input initial velocity as 3240 fps, and other data, and call it “My BB's,” I can show a chart for magical bb’s. http://www.shooterscalculator.com/ballistic-trajectory-chart.php?t=34fa8220 The Shooter’s Calculator only provides a result based on user input. It does not present a spreadsheet with the formulas to generate the data. The data from the Calculator can be cut and pasted into a spreadsheet, or entered by direct entry; this produces data in the cells, but no spreadsheet formulas in the cells. The chart states the speed of sound as 1130 feet per second (fps). The remaining 4 columns, (4, 5, 6, 7) were generated by VxH. Column 6 uses 1130.8 fps to calculate the time for sound to travel the distance stated in Column 1. Column 4 is labeled as (Avg V) Vb. This column purports to present the average velocity of the bullet to cover the distance for the row it is in. All of the data in this column is epically wrong as the methodology of calculation is absurdly wrong. To calculate the average velocity of the bullet, divide distance by time. Instead of this, a personal misbegotten formula was used. Probably a pocket calculator for each cell in Column 4 was used to perform the calculations, and the data was directly entered into the cells by hand. For the first two data rows, sum 3240 and 3163 and divide by 2. 6403/2 yields the 3201 in Column 4. For the first three data rows, sum 3240+3163+3088 for 9491. 9491 / 3 yields the 3163.6667 in Column 4. And so on, and so forth. All the calculated Column 4 data (average Vb), is garbage. The chosen methodology was to sum the velocity given for each distance, and divide by the number of elements summed. This produces nonsensical data. Example: You drive a car 100 miles at 80 mph. You drive another 100 miles at 20 mph. With this bogus methodology, 80 + 20 = 100, divide by 2, and your average velocity was 50 mph. Not. In the real world, you drove 100/80 or 1.25 hours at 80 mph. You drove 100/20 or 5 hours at 20 mph. And you drove 200 miles in 6.25 hours. Your average speed was 200/6.25, or 32 mph. Column 4, in addition to using an absurd methodology for its calculations, also incorporates two summing errors for the velocities taken from Column 3, at 900 feet and 1275 ft. In each case, the actual sum was 1 less than that calculated. Spreadsheet formulas are not prone to fat finger syndrome, and do not make such errors, but someone with a pocket calculator or pen and paper does. The data was typed in after external calculation. Where you calculate 2367.5926 average Vb at 1950 feet, 1950/1.211933 (the velocity of the bullet in Column 5), it yields 1608.9998 fps, remarkably close to the 1609 in Column 3. But then, the elapsed time in Column 2 is 0.86, not 1.21933. It is a conundrum how the bullet traveled for 1.21933 seconds in an elapsed time of 0.86 seconds. Of course, when you use Column 1 1950 ft and Column 3 1609 fps to derive the time of flight, the formula is d/Vb, and Vb is the Average Velocity. The bullet will travel 1905 feet distance (Col 1) in 0.86 sec time (Col 2) in 1905/0.86 or 2267.4418 average Vb. Stated in your headnote is Tb is d/Vb. It is noteworthy that you used Column 3 as the "average" velocity of the bullet in order to derive the other average velocity of the bullet in Column 4. Column 5 (Tb) incorporates the garbage data from Column 4 into its calculations, and all the resulting calculated data is wrong. GIGO. Column 7 (T = Tb – Ts) incorporates the garbage data from Column 5 and all the calculated data is wrong. GIGO. The chart is multicolor and pretty, but the data for the imaginary bullet is demonstrably wrong in every column you created, except for column 6 where you succeeded in dividing the distance by 1130.8.
#98. To: nolu chan (#97)
(Edited)
LOL please tell the class why the bullet accelerates / decelerates / accelerates repeatedly when your "analysis" is applied? The time in the chart rendered by the ballistic calculator only has 2 decimals of precision. Calculating the average per the reported velocity is thus more accurate.
>> and the data was directly entered into the cells by hand. Bzzzt. Fail again.
Top • Page Up • Full Thread • Page Down • Bottom/Latest
#73. To: A K A Stone, VXH, buckeroo, tooconservative, cz82, redleghunter, sneakypete, Pinguinite, Vicomte13, Liberator, Deckard (#1)
Found this interesting video.
Thread: 308 Ammo Help
This is a .223 ballistics chart (external) generated using our ballistic trajectory calculator. Based off a standard 55gr bullet leaving the barrel at 3,215fps and follows the bullet trajectory all the way to 1000 yards in steps of 50 yard increments. The charting shows the range, drop (based off a 1.5" scope mount), current velocity, energy, and time in seconds in relation to the bullets movement through space and time. This chart does not account for atmospheric conditions, so if you want to take in to effect these things check out the calculators official page. The Ballistic Coefficient for the .223 Remington, Remington Metal Case, 55gr is 0.202 (in this example) but, but may also range from .185 bc to .257
-31.7981 [drop, inches]
1588 [Velocity]
308 [energy]
532 [time, milliseconds]
#78. To: nolu chan (#73)
#81. To: VxH (#78)
All numbers he pulled out of his arse?
#82. To: nolu chan (#81)
(Edited)
The audio he used is presented.
#83. To: VxH (#82)
The amplitude graphs of the audio referenced on my meme can be reproduced by anyone with minimal tools. It's REPRODUCIBLE - that's what differentiates valid science from conspiratorial buffoonery.
#86. To: nolu chan (#83)
That you reproduce meaningless bullshit is meaningful
#88. To: VxH (#86)
The amplitude graphs are reproducible...
#89. To: nolu chan (#88)
#90. To: VxH (#89)
Maybe you just don't have what it takes.
#91. To: nolu chan (#90)
(Edited)
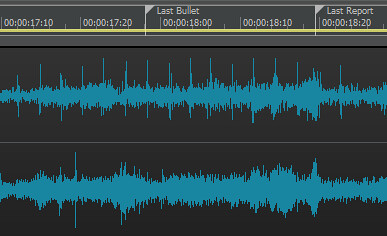
#92. To: VxH (#91)
Now, ask your donkey - what distance does that MEASURED absolute time difference correspond to on the chart?
Bullet Time, Velocity FPS, Tb–Ts
Tb = Time of bullet
Ts = Time of sound, 1.062 seconds @ 1,130 feet per second (FPS) (72ºF, 20% Humidity)
Ts – Tb = Time difference between Tb and Ts
Column 2 = Tb stepped in 100 FPS increments, beginning with Ts
Column 3 = Ts – Tb (time in seconds supersonic bullet arrives ahead of sound) Bullet time (s), Bullet average velocity (FPS), time difference to sound at 1,200 feet (s)
Bullet time (s) Bullet average vel FPS Time diff Ts-Tb 1.062 1130 0.000 0.976 1230 0.086 0.902 1330 0.160 0.839 1430 0.223 0.784 1530 0.278 0.736 1630 0.326 0.694 1730 0.368 0.656 1830 0.406 0.622 1930 0.440 0.591 2030 0.471 0.563 2130 0.499 0.538 2230 0.524 0.515 2330 0.547 0.494 2430 0.568 0.474 2530 0.588 0.456 2630 0.606 0.440 2730 0.622 0.424 2830 0.638 0.410 2930 0.652 0.396 3030 0.666 0.383 3130 0.679 0.372 3230 0.690 0.360 3330 0.702 0.350 3430 0.712 0.340 3530 0.722 0.331 3630 0.731 0.322 3730 0.740 0.313 3830 0.749 0.305 3930 0.757 0.298 4030 0.764
#93. To: nolu chan (#92)
(Edited)

#95. To: VxH (#93)
Since we KNOW from the observed audio Vb is supersonic, we can treat the difference between Tb and Ts as Absolute.
#96. To: nolu chan (#95)
(Edited)
They have a spreadsheet function for that.


#97. To: VxH (#96)

Replies to Comment # 97. 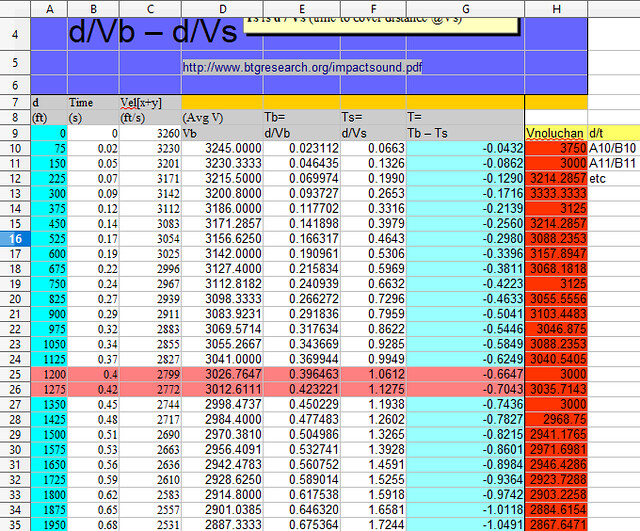
#99. To: nolu chan (#97)
(Edited)
Drag Function: G1
Ballistic Coefficient: 0.300
Bullet Weight: 62 gr
Initial Velocity: 3240 fps
Sight Height : 1.5 in
Shooting Angle: -33°Wind Speed: 0 mph
Wind Angle: 0°
Zero Range: 100 yd
Chart Range: 750 yd
Maximum Range: 50002 yd
Step Size: 25 ydCorrected For Atmosphere
Adjusted BC: 0.33
Altitude: 2000 ft
Barometric Pressure: 29.92 Hg
Temperature: 72° F
Relative Humidity: 21%
Speed of Sound: 1130 fpsRange Time Vel[x+y] (ft) (s) (ft/s) 0 0.00 3240 75 0.02 3163 150 0.05 3088 225 0.07 3014 300 0.10 2941 375 0.12 2870 450 0.15 2799 525 0.18 2730 600 0.20 2662 675 0.23 2595 750 0.26 2529 825 0.29 2465 900 0.32 2401 975 0.36 2337 1050 0.39 2275 1125 0.42 2214 1200 0.46 2154 1275 0.49 2095 1350 0.53 2036 1425 0.56 1979 1500 0.60 1923 1575 0.64 1867 1650 0.68 1813 1725 0.73 1760 1800 0.77 1708 1875 0.81 1658 1950 0.86 1609 2025 0.91 1561 2100 0.96 1515 2175 1.01 1470 2250 1.06 1426 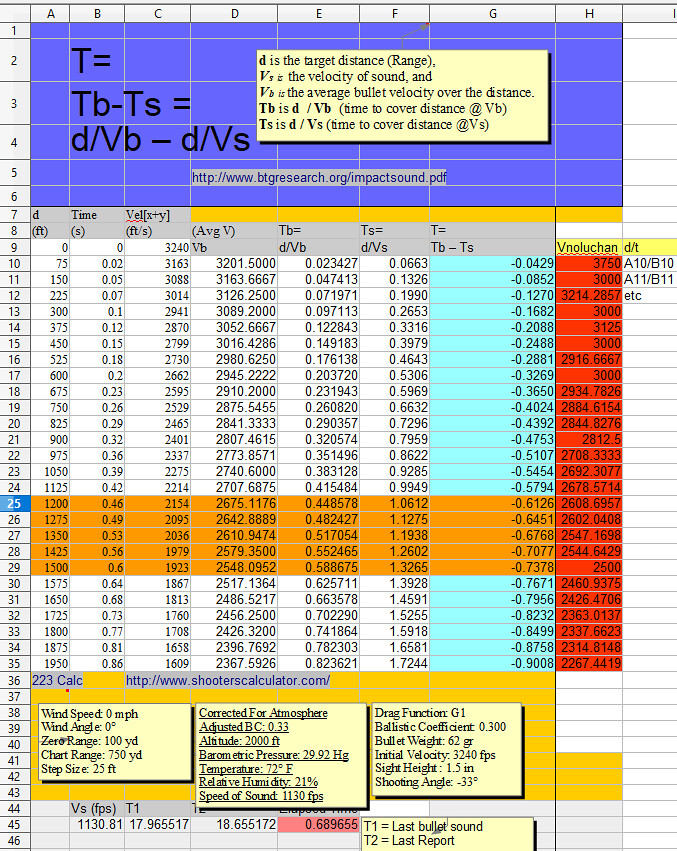

End Trace Mode for Comment # 97.
[Home] [Headlines] [Latest Articles] [Latest Comments] [Post] [Mail] [Sign-in] [Setup] [Help] [Register]
